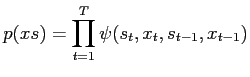

Next: Time-series cleaning: HMM-clean
Up: Hidden Markov Models, etc.
Previous: Simple Gaussian HMM
Autoregressive observations: HMM-AR
Conditional on the hidden variables
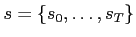 the observations
the observations
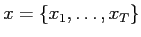 in the simple HMM, eq. (2), are independent. For time series modeling this independency is sometimes inadequate. An obvious extension is shown in Fig. 7. The
in the simple HMM, eq. (2), are independent. For time series modeling this independency is sometimes inadequate. An obvious extension is shown in Fig. 7. The 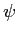 function now becomes
function now becomes
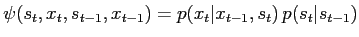 |
(31) |
and the joint distribution is
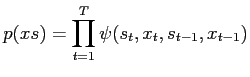 |
(32) |
where we define
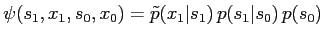 .
Again, we have forward and backward recursions for the functions
.
Again, we have forward and backward recursions for the functions
Fig.:
HMM-AR conditional dependencies.
|
|
Markus Mayer
2009-06-22