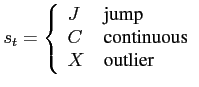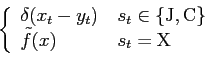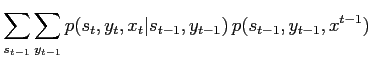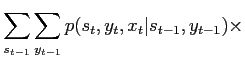
Next: Principal components: HMM-PCA Up: Hidden Markov Models, etc. Previous: Autoregressive observations: HMM-AR

Time-series cleaning: HMM-clean

Outlier cleaning of time-series requires an extension of HMM-AR, section 7: Observations are the continuos variables 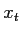. A discrete state variable 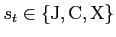$s_t\in\{\mathrm J, \mathrm C, \mathrm X\}$ represents the state of observation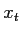

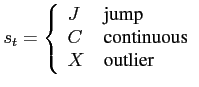$\displaystyle s_t = \left\{ \begin{array}{l l} J & \, \mbox{jump}\\ C & \, \mbox{continuous}\\ X & \, \mbox{outlier}\\ \end{array} \right.$

(35)

and a second hidden variable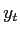

denotes the ``shadow path'' which needs to be tracked when an observed quantity is identified as an outlier. The conditional probabilities are:

$\displaystyle p(x_t\vert s_{t-1},s_t,y_{t-1},y_t)$	$\displaystyle =$	$\displaystyle p(s_t\vert s_{t-1})\,p(y_t\vert s_t,y_{t-1}) \, p(x_t\vert y_t, s_t)$
$\displaystyle p(s_t=s\vert s_{t-1} = s^\prime)$	$\displaystyle =$	$\displaystyle \pi_{s s^\prime}$
$\displaystyle p(y_t\vert s_t,y_{t-1})$	$\displaystyle =$	$\displaystyle f_{s_t}(y_t-y_{t-1})$
$\displaystyle p(x_t\vert y_t, s_t)$	$\displaystyle =$	$\begin{displaymath}\left\{ \begin{array}{l l} \delta(x_t-y_t) & \, s_t\in\{\math... ...hrm C\}\\ \tilde f(x) & \, s_t=\mathrm X\\ \end{array}\right.\end{displaymath}$	(36)

It is useful to re-factorise formulate the state probability

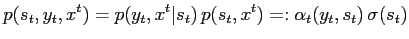$\displaystyle p(s_t,y_t,x^t) = p(y_t, x^t \vert s_t) \, p(s_t, x^t) =: \alpha_t(y_t,s_t) \, \sigma(s_t)$

(37)

because then the forward recursion becomes

$\displaystyle p(s_t,y_t,x^t)$	$\displaystyle =$	$\displaystyle \sum_{s_{t-1}}\sum_{y_{t-1}} p(s_t,y_t,x_t\vert s_{t-1},y_{t-1}) \, p(s_{t-1},y_{t-1},x^{t-1})$	(38)
	$\displaystyle =$	$\displaystyle \sum_{s_{t-1}}\sum_{y_{t-1}} p(s_t,y_t,x_t\vert s_{t-1},y_{t-1}) \times$
		$\displaystyle \quad\times\quad p(y_{t-1}, x^{t-1} \vert s_{t-1}) \, p(s_{t-1}, x^{t-1})$	(39)
	$\displaystyle =$	$\displaystyle \sum_{s_{t-1}} \underbrace{ p(s_{t-1}, x^{t-1}) }_{ \sigma_{t-1}(s_{t-1}) } \times$
		$\displaystyle \quad\times\quad \sum_{y_{t-1}} p(s_t,y_t,x_t\vert s_{t-1},y_{t-1... ...ce{ p(y_{t-1}, x^{t-1} \vert s_{t-1}) }_{ \alpha_{t-1}(y_{t-1},s_{t-1})} \quad.$	(40)

By re-factorising the update probability

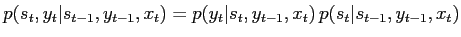$\displaystyle p(s_t,y_t\vert s_{t-1},y_{t-1},x_t) = p(y_t\vert s_t,y_{t-1},x_t) \, p(s_t\vert s_{t-1},y_{t-1},x_t)$

(41)

it is possible to sample 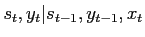$s_t,y_t\vert s_{t-1},y_{t-1},x_t$ because the two terms have a simple form:

$\displaystyle p(y_t\vert s_t,y_{t-1},x_t)$	$\displaystyle =$	$\begin{displaymath}\left\{ \begin{array}{l l} \delta(x_t-y_t) & \, s_t\in\{\math... ..._{\mathrm X}(y_t-y_{t-1}) & \, s_t=\mathrm X \end{array}\right.\end{displaymath}$	(42)
$\displaystyle p(s_t\vert s_{t-1},y_{t-1},x_t)$	$\displaystyle \propto$	$\begin{displaymath}\pi_{s_t,s_{t-1}} \left\{ \begin{array}{l l} f_{s_t}(x_t-y_{t... ...thrm C\}\\ \tilde f(x_t) & \, s_t=\mathrm X \end{array}\right.\end{displaymath}$	(43)

**Fig.:** **HMM-clean conditional dependencies.**

Next: Principal components: HMM-PCA Up: Hidden Markov Models, etc. Previous: Autoregressive observations: HMM-AR

Markus Mayer 2009-06-22