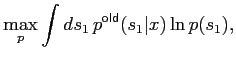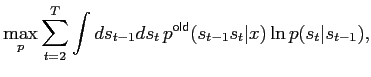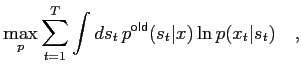

Next: Calculation of and :
Up: The general setup for
Previous: Notation
The full joint pdf of observed and hidden variables is
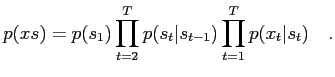 |
(2) |
The M-step in the EM algorithm amounts to finding
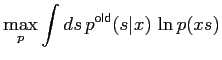 |
(3) |
and via eq (2) this is just
![$\displaystyle \max_p \int ds\, p^\mathsf{old}(s\vert x) \left[\ln p(s_1)+\sum_{t=2}^T \ln p(s_t\vert s_{t-1}) + \sum_{t=1}^T \ln p(x_t\vert s_t) \right]\quad .$](img17.png) |
(4) |
The factorization allows to maximise the three terms inpedendently,
i.e. the quantities
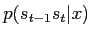 and
and 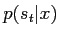 have to be calculated. Introduce the following
shorter notation for these:
have to be calculated. Introduce the following
shorter notation for these:


Next: Calculation of and :
Up: The general setup for
Previous: Notation
Markus Mayer
2009-06-22
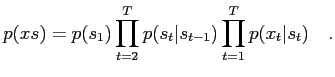
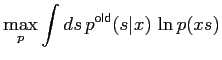
![$\displaystyle \max_p \int ds\, p^\mathsf{old}(s\vert x) \left[\ln p(s_1)+\sum_{t=2}^T \ln p(s_t\vert s_{t-1}) + \sum_{t=1}^T \ln p(x_t\vert s_t) \right]\quad .$](img17.png)