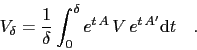

Next: Conditional finite-time yield dynamics
Up: Properties of the term
Previous: Instantaneous covariances
With the process for the zero-rates given in (![[*]](crossref.png) ), the integration
can be carried out to obtain the finite-time differences:
), the integration
can be carried out to obtain the finite-time differences:
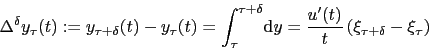 |
(16) |
Unconditional expectation and variance are
The finite-time covariance 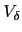 is given in section
is given in section
![[*]](crossref.png) as
as
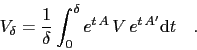 |
(17) |
Markus Mayer
2009-06-22
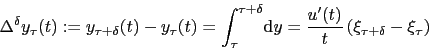
![[*]](crossref.png) ), the integration
can be carried out to obtain the finite-time differences:
), the integration
can be carried out to obtain the finite-time differences:
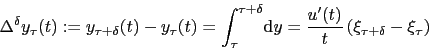
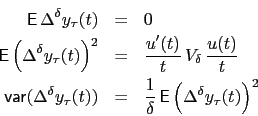
![[*]](crossref.png) as
as