Conditional finite-time yield dynamics

Next: The forward curve Up: Properties of the term Previous: Unconditional finite-time yield dynamics

Conditional finite-time yield dynamics

Define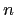

zero-rates ${\mathsf y_{\mathrm{kr}}}$ as key rates, then ${\mathsf y_{\mathrm{kr}}}= \mathsf U_{\mathrm{kr}}\,\xi-{\mathsf v}$ , i.e. arbitrary rates ${\mathsf y}=\mathsf U\,\xi-{\mathsf v}$ can be reexpressed in terms of the key-rates

$\begin{displaymath} {\mathsf y}= \mathsf U\mathsf U_{\mathrm{kr}}^-({\mathsf y_{\mathrm{kr}}}+{\mathsf v})-{\mathsf v} \end{displaymath}$

(18)

and the conditional yield change ${\Delta\mathsf y}\vert{\mathsf y_{\mathrm{kr}}}_0 := {\mathsf y}_t-{\mathsf y}_0\vert{\mathsf y_{\mathrm{kr}}}_0$ is

$\begin{eqnarray*} \mathsf E\left[{\Delta\mathsf y}\vert{\mathsf y_{\mathrm{kr}}... ...^-({\mathsf y_{\mathrm{kr}}}_0+{\mathsf v})-\mu_\infty) \quad , \end{eqnarray*}$

i.e. $E\left[{\Delta\mathsf y}\vert{\mathsf y_{\mathrm{kr}}}_0\right]$ is affine in ${\mathsf y_{\mathrm{kr}}}_0$ :

$\begin{displaymath} E\left[{\Delta\mathsf y}\vert{\mathsf y_{\mathrm{kr}}}_0\ri... ...athsf U_{\mathrm{kr}}^-{\mathsf v}-\mu_\infty)\right] \quad . \end{displaymath}$

(19)

Markus Mayer 2009-06-22