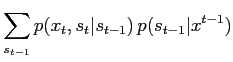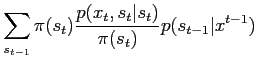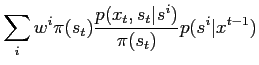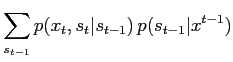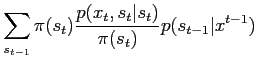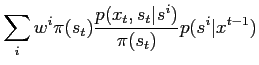

Next: Backward sampling
Up: Monte-Carlo approaches
Previous: Exact forward sampling
If evaluation of
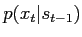 or sampling from
or sampling from
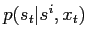 is difficult or impossible
alternative sampling methods can be obtained. Start again with the forward
recursion (10) in the following form
is difficult or impossible
alternative sampling methods can be obtained. Start again with the forward
recursion (10) in the following form
Markus Mayer
2009-06-22