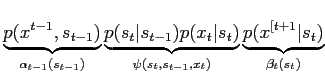

Next: Recursion for conditional distributions:
Up: The general setup for
Previous: Max-likelihood inference and EM-Algorithm
Calculation of  and
and  : Sum-product derivation
: Sum-product derivation
Key to efficient calculation of any quantity in the HMM is the fact that the summations over hidden variables can be 'pulled' out. Rewrite the full joint eq. (2):
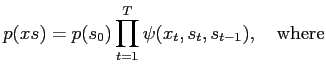 |
|
|
(6) |
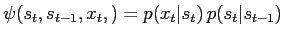 |
|
|
(7) |
and the summations over the hidden variables
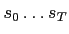 can be regrouped
can be regrouped
One term in the sequence of sums is
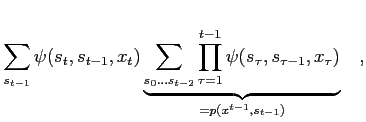 |
(8) |
so with the definition
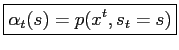 |
(9) |
we obtain the forward recursion
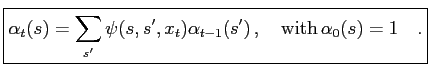 |
(10) |
Similarly, the summations for 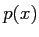 can be arranged backward:
can be arranged backward:
With the introduction of
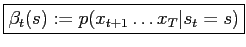 |
(11) |
we obtain the backward recursion
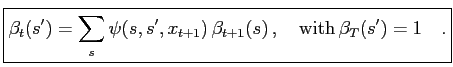 |
(12) |
Fig.:
Graphical representation of 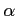
|
|
Fig.:
Graphical representation of 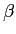
|
|
The desired quantities
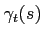 and
and
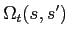 defined in eq. (5) can be expressed in terms of
defined in eq. (5) can be expressed in terms of  and
and  .
Observe that
.
Observe that


Next: Recursion for conditional distributions:
Up: The general setup for
Previous: Max-likelihood inference and EM-Algorithm
Markus Mayer
2009-06-22
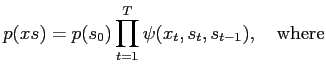
![]() can be regrouped
can be regrouped
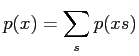
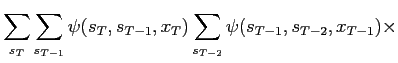
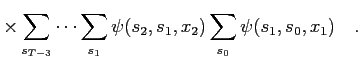
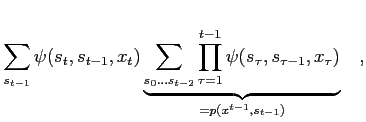
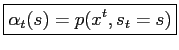
![]() can be arranged backward:
can be arranged backward:
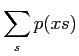
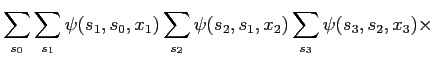
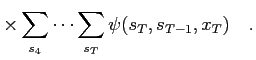
![]() and
and
![]() defined in eq. (5) can be expressed in terms of
defined in eq. (5) can be expressed in terms of ![]() and
and ![]() .
Observe that
.
Observe that