

Next: Alternative forward sampling
Up: Monte-Carlo approaches
Previous: Monte-Carlo approaches
Start again with the forward recursion (10)
and reformulate as
Approximate
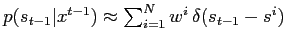 with
with
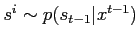 and
and
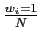 , then
, then
The normalisation is just
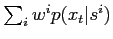 , so for we can sample from
, so for we can sample from
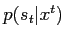 according
to this algorithm:
according
to this algorithm:
This requires to evaluate
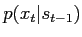 and sample from
and sample from
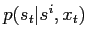 .
I.e. the algorithm generates a sequence of swarms of `particles'
.
I.e. the algorithm generates a sequence of swarms of `particles'
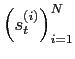 by recursively sampling according to (24).
by recursively sampling according to (24).


Next: Alternative forward sampling
Up: Monte-Carlo approaches
Previous: Monte-Carlo approaches
Markus Mayer
2009-06-22
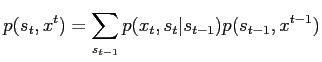
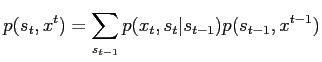
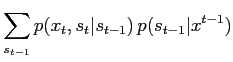
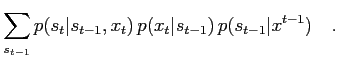
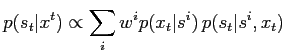
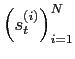 by recursively sampling according to (24).
by recursively sampling according to (24).