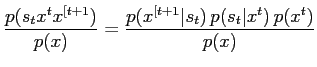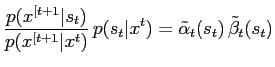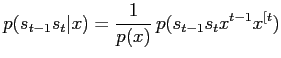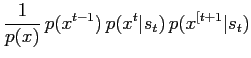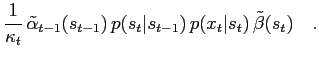

Next: Monte-Carlo approaches
Up: The general setup for
Previous: Calculation of and :
Recursion for conditional distributions: The Baum-Welch Algorithm
The recursion of section 1.3 have serious underflow problems in numerical
applications, and 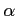 and
and 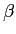 do not represent useful variables. Introduce forward and backward variables
do not represent useful variables. Introduce forward and backward variables
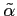 and
and
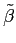 :
:
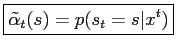 |
(13) |
which allows to write
so the recursion is
The new variable 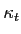 is just the normalizing constant for
is just the normalizing constant for
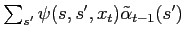 , therefore
, therefore
Next, normalise 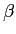 as follows:
as follows:
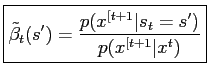 |
(19) |
and, using (19) and (12) the backward recursion for
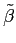 becomes
becomes
Because of
the recursion becomes
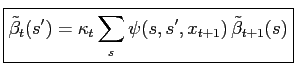 |
(22) |
Since
the backward iteration is properly initialised by defining
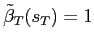 |
(23) |
Finally, the desired quantities 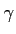 and
and 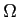 in the M-step are related to
in the M-step are related to
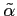 and
and
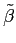 via
via
and


Next: Monte-Carlo approaches
Up: The general setup for
Previous: Calculation of and :
Markus Mayer
2009-06-22
![]() and
and ![]() do not represent useful variables. Introduce forward and backward variables
do not represent useful variables. Introduce forward and backward variables
![]() and
and
![]() :
:
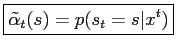
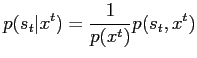
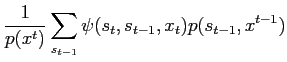
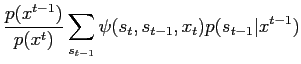
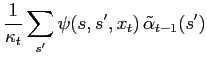
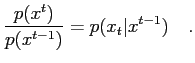
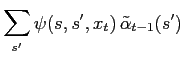
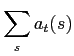
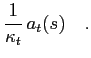
![]() as follows:
as follows:
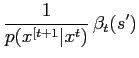
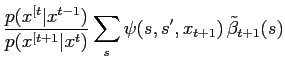
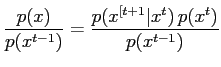
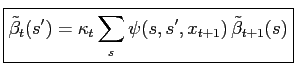
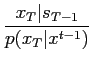
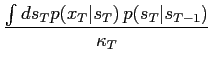
![]() and
and ![]() in the M-step are related to
in the M-step are related to
![]() and
and
![]() via
via