

Next: Bibliography
Up: Model specification - EFM(1)
Previous: Diagonalisation of and
In this section we toggle the superscript stars  towards a slimmer notation, i.e. in this section the risk neutral parameters carry no star whereas the objective measure parameters obtain the
towards a slimmer notation, i.e. in this section the risk neutral parameters carry no star whereas the objective measure parameters obtain the  . I.e. now
. I.e. now
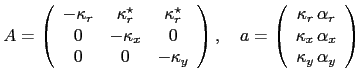 |
|
|
(106) |
The usual ansatz
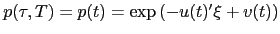 leads to the following two ODEs
leads to the following two ODEs
The function 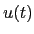 has a natural interpretation as duration with respect to the rates
has a natural interpretation as duration with respect to the rates 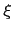 , since
, since
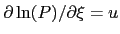 .
The first ODE can be solved right away,
.
The first ODE can be solved right away,
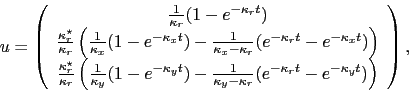 |
(109) |
solving the second ODE amounts to integration over 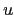 and
and 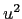 terms. To do this simplify notation:
terms. To do this simplify notation:
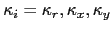 , i.e.
, i.e. 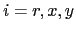 . Introduce the two functions
. Introduce the two functions
which gives 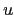 as
as
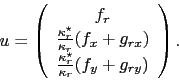 |
(112) |
The limiting cases of 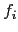 and
and 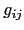 must be taken into account:
must be taken into account:
Five integrals are required (the 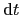 's in
's in 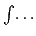 are implicit throughout):
are implicit throughout):
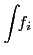 |
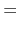 |
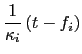 |
(115) |
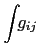 |
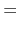 |
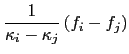 |
(116) |
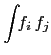 |
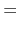 |
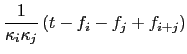 |
(117) |
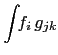 |
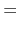 |
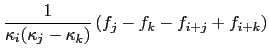 |
(118) |
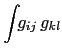 |
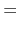 |
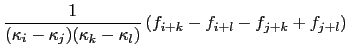 |
(119) |
where the subscript 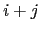 stand for
stand for
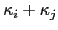 , etc.
Four limiting cases need to be considered:
, etc.
Four limiting cases need to be considered:
In terms of the five integrals 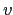 can be integrated to (set
can be integrated to (set
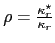 )
)
Note that
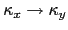 is not a singularity of
is not a singularity of 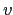 .
Table
.
Table ![[*]](crossref.png) summarizes the correct combinations.
From the viewpoint of computational effectiveness calculate the quantities in the following order:
summarizes the correct combinations.
From the viewpoint of computational effectiveness calculate the quantities in the following order:
-
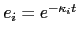
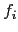
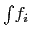
-
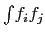
-
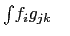 :
:
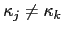 :
:
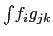
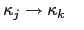 :
:
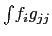
-
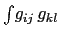 :
:
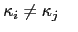 :
:
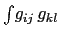
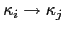 :
:
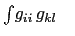
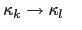 :
:
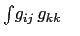
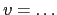
Table:
Integrating the 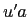 and
and 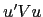 -term
-term
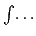 |
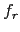 |
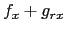 |
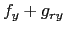 |
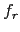 |
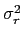 |
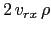 |
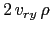 |
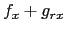 |
|
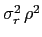 |
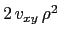 |
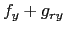 |
|
|
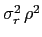 |


Next: Bibliography
Up: Model specification - EFM(1)
Previous: Diagonalisation of and
Markus Mayer
2009-06-22
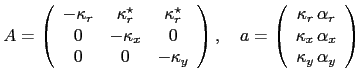
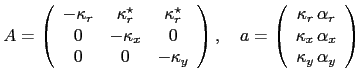
![]() leads to the following two ODEs
leads to the following two ODEs
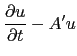
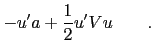
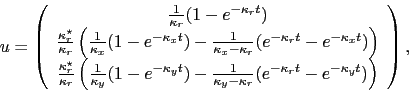
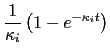
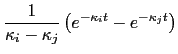
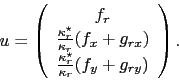
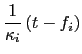
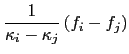
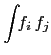
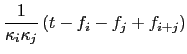
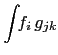
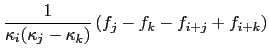
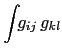
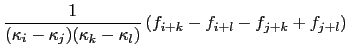
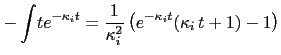
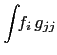
![$\displaystyle \frac{1}{\kappa_i}\left[\int\!\! g_{ii}-\int\!\! g_{i+j,i+j}\right]$](img321.png)
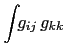
![$\displaystyle \frac{1}{\kappa_i-\kappa_j}\left[\int\!\! g_{i+k,i+k}-\int\!\! g_{j+k,j+k}\right]$](img323.png)
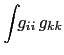
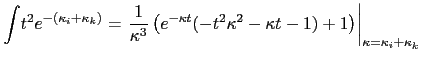
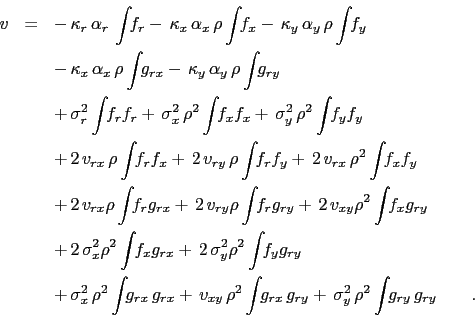
![[*]](crossref.png) summarizes the correct combinations.
From the viewpoint of computational effectiveness calculate the quantities in the following order:
summarizes the correct combinations.
From the viewpoint of computational effectiveness calculate the quantities in the following order: