

Next: Bond portfolios
Up: The general -factor Gaussian
Previous: The forward curve
The instantaneous conditional expected excess return is
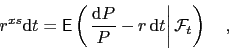 |
(24) |
with
Since
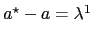 ,
,
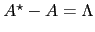 the conditional expected excess return is
the conditional expected excess return is
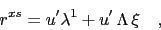 |
(25) |
and the conditional instantaneous excess return variance is
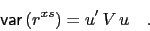 |
(26) |
For a choice of 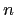 key rates
key rates
 the conditional expected excess return is
the conditional expected excess return is
Markus Mayer
2009-06-22
![\begin{eqnarray*}
\frac{\mathrm{d}P}{P} &=& \frac{\mathrm{d}u^\prime}{\mathrm{d...
...\left[\lambda(\xi)\,\mathrm{d}t-\Sigma\mathrm{d}W\right]\quad .
\end{eqnarray*}](img96.png)
![\begin{eqnarray*}
\mathsf E\left[r^{xs}\vert{\mathsf y_{\mathrm{kr}}}\right]
...
...sf U\Lambda\mathsf U_{\mathrm{kr}}^- {\mathsf v}\right] \quad .
\end{eqnarray*}](img101.png)