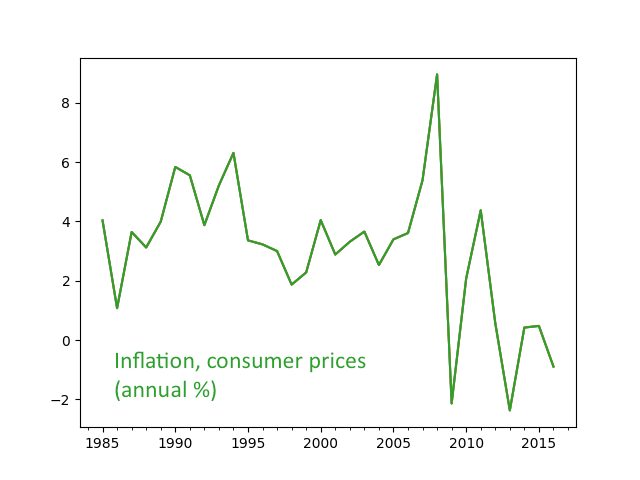
The Kelly criterion and fixed fraction betting is briefly introduced and extended to left bounded profit/loss distributions (i.e. profit/loss distributions that are bounded from the left). Various inequalities are studied and analytical tools are offered. Click here for the full text.
Introduction
Let $X$ be a real random variable with support $[-1,\infty[$. Following Kelly [1] consider the reinvested growth of a fixed fraction investment in an instrument that has payoff $X$.
$$W_n = W_{n-1}(1+\alpha\,X_n), \quad X_n \sim X, \alpha\in[0,1]\quad.$$
(If the support of $X$ is bounded the restriction on $\alpha$ can be relaxed.)
The long run growth rate is
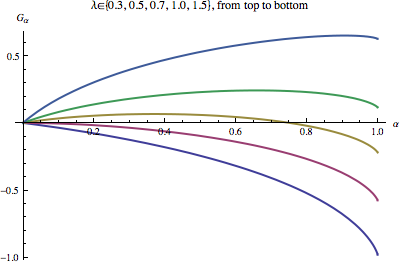
$$G_\alpha = \lim_{N\rightarrow\infty} \frac{1}{N} \log\frac{W_N}{W_0}\quad.$$
By the law of large numbers
$$G_\alpha = \mathsf{E} \log(1+\alpha\,X) \quad\mathrm{a.s.}\quad.$$
For a given $X$ the function $G_\alpha$ is concave in $\alpha$, and, writing $G'(\alpha)=dG/d\alpha$ we have $G'(0)=E X$.
Define the maximal growth rate as
$$G[X] = \max_\alpha\,\mathsf{E} \log(1+\alpha\,X)\quad.$$
$G[X]$ and $\mathsf{E} X$
Since the slope of $G_\alpha$ at $\alpha=0$, i.e. $G'(0)=\mathsf{E} X$, determines the location of the maximum we have, for $\alpha\in[0,1]$,
$$\mathsf{E} X\leq0 \Leftrightarrow G[X]=0, \alpha_\mathrm{opt}=0,$$
and
$$E X>0 \Leftrightarrow G[X]>0, \alpha_\mathrm{opt}>0$$
Upper bound for $G[X]$
Jensen’s inequality yields
$G_\alpha \leq \log(1+\alpha {{\mathsf{E}}}X)$ and because of $\alpha<1$
and $\log(1+x) \leq x$ it is
$$\label{eq:ineq1} G[X] \leq \log(1+{{\mathsf{E}}}X) \leq {{\mathsf{E}}}X \quad .$$
Mixtures
Consider a mixture $p(X)=\int dY p(X|Y)p(Y)$. ...
Click here for the full text.