next up previous
Next: The shifted exponential distribution Up: Analytical solutions for Previous: Analytical solutions for

Binomial distribution $ \pi $

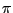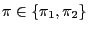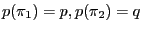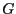For a binomial distribution $ \pi $ with $ \pi\in\{\pi_1,\pi_2\}$ , $ p(\pi_1)=p, p(\pi_2)=q$ gain $ G$ can be readily found:

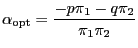$\displaystyle \alpha_\mathrm{opt} = \frac{-p \pi _1-q \pi _2}{\pi _1 \pi _2}$ (13)

and

$\displaystyle G[\pi] = p \log \left(p\,\frac{\pi_2-\pi_1}{\pi_2}\right)+q\,\log\left(q\frac{\pi_2-\pi_1}{-\pi_1}\right)$ (14)

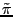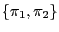The fair odds distribution $ \tilde\pi$ on $ \{\pi_1,\pi_2\}$ , for which 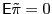$ {\mathsf{E}}\tilde\pi=0$ is

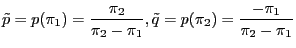$\displaystyle \tilde p = p(\pi_1)=\frac{\pi_2}{\pi_2-\pi_1}, \tilde q = p(\pi_2)=\frac{-\pi_1}{\pi_2-\pi_1}$ (15)

And therefore

$\displaystyle G[\pi] = p \log\frac{p}{\tilde p} + q \log\frac{q}{\tilde q} = \mathrm{KL}(\tilde q\vert\vert p)$ (16)


Markus Mayer 2010-06-04