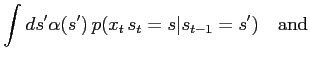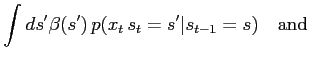

Next: Discrete HMM
Up: Hidden Markov Models, etc.
Previous: EM-Algorithm
From a slightly more general point of view the HMM can be defined by the initial and
transition probabilities
and the forward/backward recursion still hold (although the factorization in the M-step of the EM-algorithm
fails). The defining probabilities are feasible for the recursions if 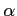 and
and 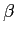 are stable under
the updating equations:
are stable under
the updating equations:
where 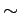 means that left-hand side and right-hand side are of the same familiy of distributions.
means that left-hand side and right-hand side are of the same familiy of distributions.
Markus Mayer
2009-06-22