

Next: Model specification - EFM(1)
Up: EFM and a class
Previous: Non-stationary OU-processes
Diagonalisation of outer product matrices
For any
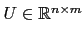 the matrix
the matrix
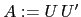 is symmetric with real eigenvalues.
Write
is symmetric with real eigenvalues.
Write
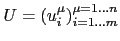 . We are looking for eigenvectors
. We are looking for eigenvectors 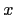 to eigenvalue
to eigenvalue  ,
i.e.
,
i.e.
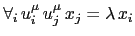 . The ansatz
. The ansatz
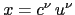 leads to
leads to
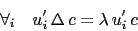 |
(90) |
with
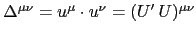 . If
. If 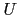 has maximal rank, this is equivalent to
has maximal rank, this is equivalent to
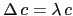 , i.e. it suffices to diagonalise
, i.e. it suffices to diagonalise
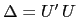 . The linear space
. The linear space
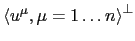 is the eigenspace to eigenvalue
is the eigenspace to eigenvalue 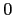 . The matrix
. The matrix
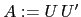 has
exactly
has
exactly 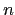 (degeneracies counted) non-zero eigenvalues.
(degeneracies counted) non-zero eigenvalues.
Markus Mayer
2009-06-22