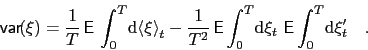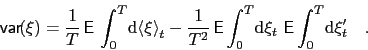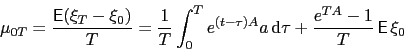

Next: Estimation of OU processes
Up: OU-processes
Previous: Autocorrelation function and power
If the relaxation time (the inverse of the smallest eigenvalue) is larger than the observation time
the estimation of the unconditional momenta must be corrected. In the limit of continuous observation
of the process
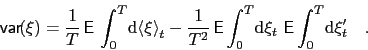 |
(83) |
The first term in the sum is just the instantaneous variance
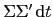 . The correction
to the instantaneous conditional variance is therefore (define the sample mean
. The correction
to the instantaneous conditional variance is therefore (define the sample mean
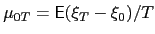 )
)
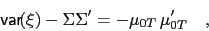 |
(84) |
i.e. the unconditional process variance has to be adjusted down.
The sample mean is
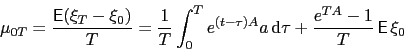 |
(85) |
In the limit 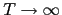 this simplifies to
this simplifies to
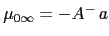
Markus Mayer
2009-06-22