

Next: Autocorrelation function and power
Up: OU-processes
Previous: OU-process in VAR form
Denote the 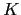 observations of the process at times
observations of the process at times 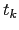 by
by
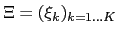 . The probability of observation
. The probability of observation 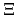 given parameters
given parameters
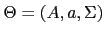 is
is
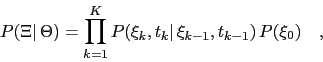 |
(74) |
and, up to a parameter-independent constant, the log-likelihood function is
![\begin{displaymath}
l(\Theta) = -{1\over 2}\sum_{k=2}^K\left[\det(V_{\Delta_k})...
...a_k}^- (\Delta\xi_k-\mu_{t_k\vert\,t_{k-1}})
\right]\quad ,
\end{displaymath}](img215.png) |
(75) |
where
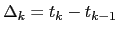 and
and
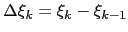 .
.
Markus Mayer
2009-06-22
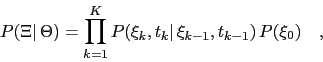
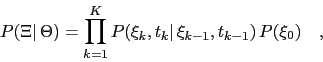
![\begin{displaymath}
l(\Theta) = -{1\over 2}\sum_{k=2}^K\left[\det(V_{\Delta_k})...
...a_k}^- (\Delta\xi_k-\mu_{t_k\vert\,t_{k-1}})
\right]\quad ,
\end{displaymath}](img215.png)