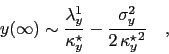

Next: Short-end slope
Up: Special results for EFM(2)
Previous: u(t)
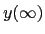
The results of section ![[*]](crossref.png) apply and special expressions for the
specification EFM(2) can be obtained. First,
apply and special expressions for the
specification EFM(2) can be obtained. First,
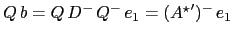 has a simple expression:
has a simple expression:
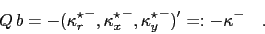 |
(62) |
This leads to
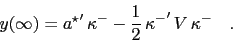 |
(63) |
The long yield 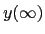 is dominated by the smallest mean reversion strength (under
is dominated by the smallest mean reversion strength (under  ).
For
).
For
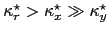 and
and
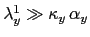 it scales with
it scales with
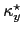 as
as
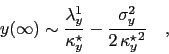 |
(64) |
i.e. the blow-up effect of
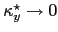 can only be compensated by
can only be compensated by
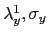 of the order of
of the order of
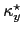 .
.
Markus Mayer
2009-06-22
![[*]](crossref.png) apply and special expressions for the
specification EFM(2) can be obtained. First,
apply and special expressions for the
specification EFM(2) can be obtained. First,