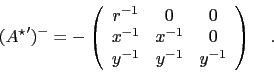

Next: Special results for EFM(2)
Up: EFM(2)
Previous: Model specification
Diagonalisation of
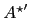 is possible for
is possible for
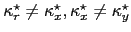 .
For ease of notation, write
.
For ease of notation, write
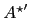 as follows:
as follows:
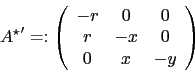 |
(54) |
The eigenvalues are 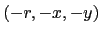 with eigenvectors (
with eigenvectors (
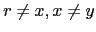 )
)
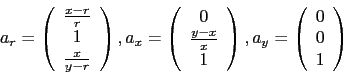 |
(55) |
Introduce
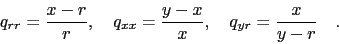 |
(56) |
For
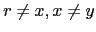 diagonalisation is possible,
diagonalisation is possible,
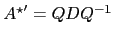 ,
with
,
with
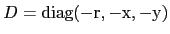 and
and
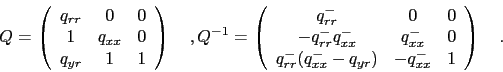 |
(57) |
Similarly, the diagonalisation of
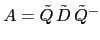 is achieved.
Write
is achieved.
Write 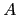 in short notation,
in short notation,
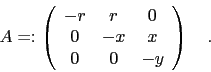 |
(58) |
Then using the result for
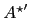 it is
it is
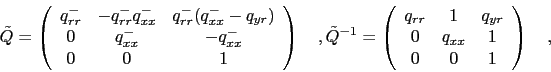 |
(59) |
where
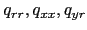 defined as above except with
defined as above except with 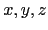 the entries of matrix
the entries of matrix 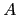 .
.
The inverse of
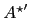 will be needed, too:
will be needed, too:
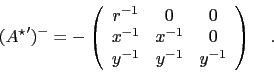 |
(60) |


Next: Special results for EFM(2)
Up: EFM(2)
Previous: Model specification
Markus Mayer
2009-06-22
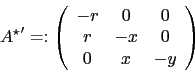
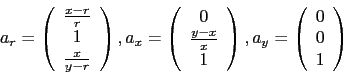
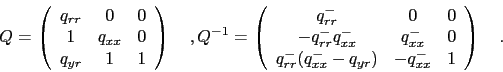
![]() is achieved.
Write
is achieved.
Write ![]() in short notation,
in short notation,
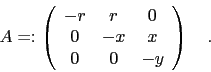
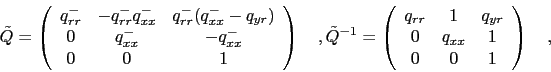
![]() will be needed, too:
will be needed, too: