Partial yield curve inversion using linearity in some parameters

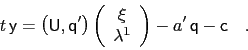
Next: Sensitivity of yields to Up: The general -factor Gaussian Previous: Sensitivity of prices and

Partial yield curve inversion using linearity in some parameters

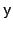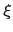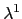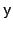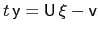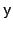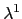Yields ${\mathsf y}$ are affine in state variables $\xi$ and constant risk premia $\lambda^1$ . (As usual ${\mathsf y}$ represents the yield curve as a vector of yields at selected maturities.) Write again $t\,{\mathsf y}= \mathsf U\,\xi-{\mathsf v}$ . Linearity of ${\mathsf y}$ in $\lambda^1$ enters through 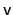${\mathsf v}$ . 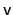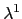Rewrite ${\mathsf v}$ by splitting it into the parts linear and constant in $\lambda^1$ ,

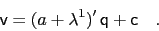$\begin{displaymath} {\mathsf v}= (a+\lambda^1)^\prime\,\mathsf q+\mathsf c\quad . \end{displaymath}$

(37)

Then altogether

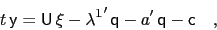$\begin{displaymath} t\,{\mathsf y}= \mathsf U\,\xi-{\lambda^1}^\prime\,\mathsf q- a^\prime\,\mathsf q-\mathsf c\quad , \end{displaymath}$

(38)

and the following linear problem has to be solved:

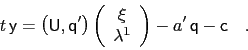$\begin{displaymath} t\,{\mathsf y}= \left(\mathsf U, \mathsf q^\prime\right) ... ...1 \end{array} \right) -a^\prime\,\mathsf q-\mathsf c\quad . \end{displaymath}$

(39)

Depending on the number of maturities observed the inversion can either be done exactly or a linear fit can be sought. Some entries of 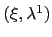$(\xi, \lambda^1)$ can also be prespecified and be moved into the constant part.

Markus Mayer 2009-06-22